|
Go to 1 2 3
______________________ 3. Mathematics vs Physics. Fictitious time or physical time? Experimental evidence? << Since the mathematicians have invaded the theory of relativity, I do not understand it myself anymore. >> Quoted in P A Schilpp, Albert Einstein, Philosopher-Scientist (Evanston 1949). << Einstein maintained his views on the appropriate place of mathematics in physical theory until the end of his life. A close physician friend of Einstein’s in the 1920s clarified how Einstein remained suspicious of mathematical formalism. Einstein remarked on a problem that he had come up against: "I’m afraid I’m wrong again. I can’t put my theory into words. I can only formulate it mathematically, and that’s suspicious.">> J Plesch, Janos (ref 29) p 208. An interesting Einstein quote from his discussion with Lemaître regarding the expanding universe. Einstein told him: "Your math is correct, but your physics is abominable". (Sometimes quoted as: "Your calculations are correct, but your grasp of physics is abominable." (Lemaitre finally turned out to be correct, but that's off topic here.) Lorentz faced the same problem between mathematics and physics: (my bold) << The chief cause of my failure was my clinging to the idea that the variable t only can be considered as the true time and that my local time t' must be regarded as no more than an auxiliary mathematical quantity. In Einstein's theory, on the contrary, t' plays the same part as t; if we want to describe phenomena in terms of x'; y'; z'; t' we must work with these variables exactly as we could do with x; y; z; t. >> Lorentz, H.A (1916), The theory of electrons, Leipzig & Berlin: B.G. Teubner. In LET the time coordinates of the moving system are fictitious. They have no physical meaning. This is a well documented issue. For example here. A few quotes (bold is mine): Chapter 3. P4: <<Many authors (e.g., Goldberg, Miller, Schaffner) have claimed that Lorentz looked upon the Lorentz transformed quantities playing a role in the theorem of corresponding states as the quantities measured by the moving observer. It is true that, under the influence of Einstein’s work, Lorentz would eventually come to adopt that interpretation, but it is completely foreign to his thinking prior to 1905. Before 1905, the Lorentz transformed quantities were no more than mathematical auxiliaries for Lorentz. >> P16 << That the quantities t′, x′, E′, and B′ were just mathematical auxiliaries for Lorentz with no physical meaning is illustrated by the last paragraph of this section, which, in my notation, can be paraphrased as: ... >> P16 << However, as I already emphasized, for Lorentz these primed quantities were no more than mathematical auxiliaries. Before 1905, Lorentz tacitly assumed that the moving observer would measure the Galilean transformed quantities of the frame S. >> P17 <<... will give the fictitious fields E′ and B′ as a function of the coordinates x = x′ of S and the local time t′ for the corresponding state of that configuration...>> P83 << 3.5 Lorentz’s interpretation of the Lorentz transformation formulae after 1905: from mathematical auxiliaries to effective coordinates and fields. >> P89 << 3.5.4 Lorentz taking to heart a lesson from Einstein (after ignoring a similar lesson from Poincaré). >> P89 << Giving full credit to Einstein, Lorentz explained that these quantities are not just mathematical auxiliaries, convenient for carrying out calculations in coordinate systems moving with respect to the ether, but that they actually represent the measured -or “effective” (ibid, p. 223)- quantities for observers moving along with such coordinate systems. In the light of recent work by Darrigol (1994b), showing that Poincaré had been using this physical interpretation of the quantities in Lorentz’s theorem of corresponding states at least since 1900, it is somewhat puzzling that Lorentz only started pursuing this interpretation after he had read Einstein’s work. At this point, I can only speculate what it was about Einstein’s work that suddenly made Lorentz see the fruitfulness of a physical interpretation that had been available to him for several years through the work of Poincaré. My guess is that it has to do with the fact that Einstein made the physical interpretation of the Lorentz transformation the basis for a remarkably clear and simple discussion of the electrodynamics of moving bodies, whereas Poincaré’s remarks on the physical interpretation of Lorentz transformed quantities may have struck Lorentz as inconsequential philosophical asides in expositions that otherwise closely followed his own. I also have a sense that Lorentz found Einstein’s physically very intuitive approach more appealing than Poincaré’s rather abstract but mathematically more elegant approach. ...>> P91 << If I had to write the last chapter now, I should certainly have given a more prominent place to Einstein’s theory of relativity [...] by which the theory of electromagnetic phenomena in moving systems gains a simplicity that I had not been able to obtain. The chief cause of my failure was my clinging to the idea that the variable t only can be considered as the true time and that my local time t′ must be regarded as no more than an auxiliary mathematical quantity. >> (Lorentz 1916, p. 321, note 72*) >> Lorentz, H.A (1916), The theory of electrons, Leipzig & Berlin: B.G. Teubner P91 << There is not the slightest hint in Lorentz’s work prior to 1905 as to how the second xdependent term in the expression for t′ might be given a physical interpretation. >> The difference between fictitious and real is crucial to understand the difference between the inexistent observational evidence of LT in LET and the real observational evidence of LT in SR. Many people are not aware of this crucial fact. Especially LET adepts tend to 'forget' this crucial point when putting forward and defending LET as a valid equal alternative for Special Relativity. Their argument is that because the LT give the same mathematical results in LET and SR both theories are valid physical interpretations of the LT. As if there is no difference between a 3D theory with fictitious 'moving' time such as in LET, and the 4D theory of SR where the proper time coordinates are physically real time clock indications! ____________________________________________________ <==
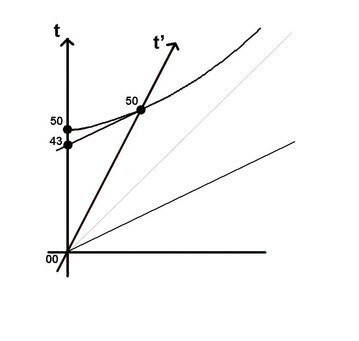
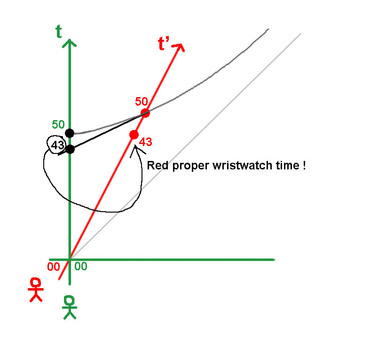
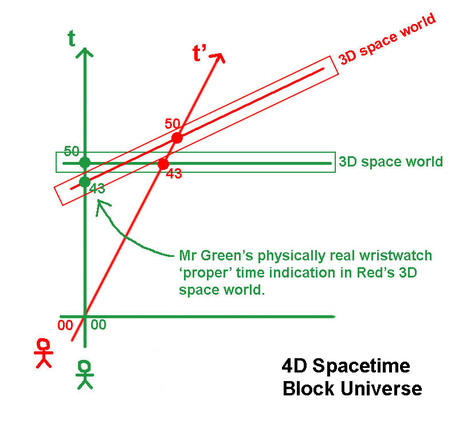
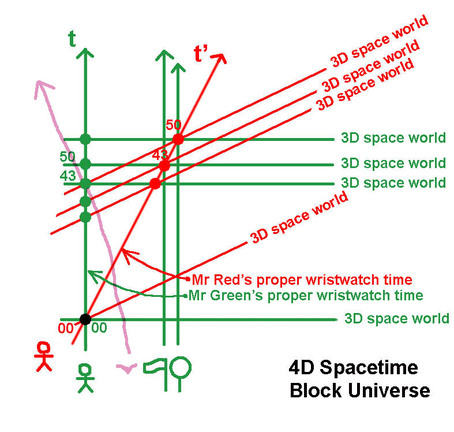
Let me show you how mathematicians tend to forget about physical meaning. The sketch shows you how mathematicians will visualize the moving clock's time slowing down. Mr Green considers himself stationary. Mr Red and his clock move relative to him at speed 0;5c. In a Minkoswki diagram the length of time (and space) units on the axes are not equal. To calibrate them we introduce a hyperbole. In the stationary frame the t'=50 is read as 43. Full stop. Mathematicians will tell you that's exactly what their calculator tells them when they throw t=50 in the time dilation formula. I think it fair to ask what that '43' stands for. If it is a measured quantity, an observation of an observation independent physically real wristwatch time indication, then it has to be a physically real clock with hands pointing to number 43. That clock has to be located somewhere in physical space, hence physically simultaneous with green clock showing 50. The diagram does not show you how that works! But, believe it or not, mathematicians don't bother. They got the mumbers and are happy. The diagram shown is a mathematical model, a geometric system showing the 50 'changing', or 'transforming' into 43. The result of a LT calculation. (If you want more of this type of mathematical diagrams Click here. ) Does that give you a clear picture of a physically real 3D world out there? Ask mathematicians what such a mathematical diagram means in real 3D world and they will panic, because... they do not know! And they do not know because they have not grasped the physical interpretation of 4D spacetime. No wonder there are thousand of books erroneously telling you that a moving clock 'seems' (or 'appears') to slow down! I bet not one of those authors know how 4D spacetime works. I will show you what the 43 time really means in the physically real 3D world. ____________________________________________________ <==
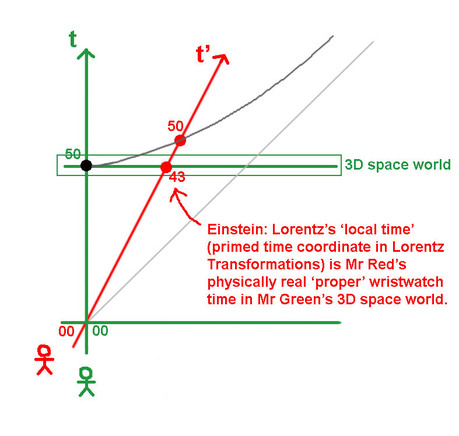
The 43 is a real clock time indication of the moving clock, nothing else than a clock event a little bit before the event red clock 50 on the world line of the red clock. ____________________________________________________ <==
That clock, physically real time indication on Mr Red's wristwatch, is what is present in Mr Green's 3D space world when his clock shows 50. ____________________________________________________ <==
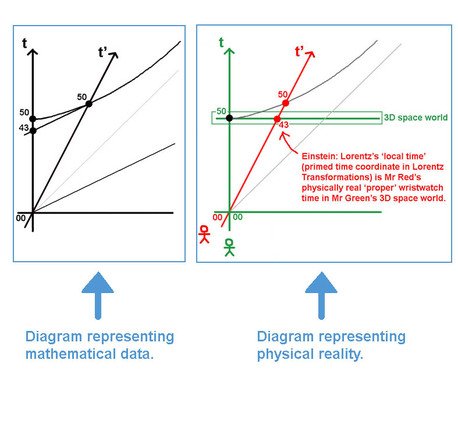
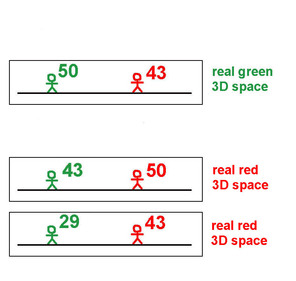
Compare the mathematical diagram with the physical representation and you see the difference between mathematics and physics. ____________________________________________________ <==
It gets even more interesting when we add the slowing down of Mr Green's clock time as observed by Mr Red. Two different 3D worlds with different physically real clock time indication. It only makes sense when the different 3D worlds co-exist in a bigger structure: 4D Spacetime, Block Universe. If you tell me that there are no different 3D worlds, but only mathematical data measured from one and the same (absolute) 3D world, then the simultaneity of the events of that 3D world (3D world = 3D space of simultaneous events) is not physical either. In other words there is no physical 3D world either. But then what is out there that you are measuring? LET fanatics and fundamentalist mathematicians do not understand that SR's 4D Spacetime has a physical meaning. That's Einstein's discovery: different frames are physically real 3D worlds in which the physical laws are equally valid. Different 3D worlds, but all part of one invariant 4D Block Spacetime Universe. ____________________________________________________ <==
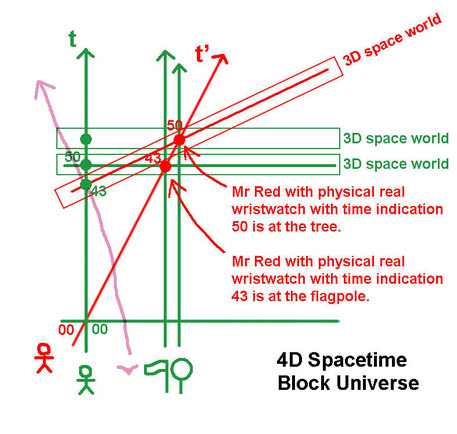
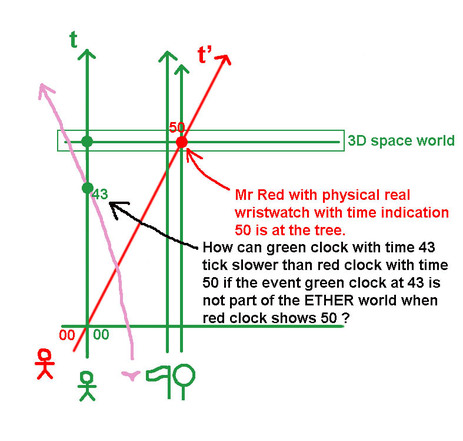
I agree that the lines and dots on a spacetime diagram are a bit abstract. Probably too abstract for mathematicians to see what they really represent. To make sure you see different physically real events in the diagram I introduce the worldlines of a flagpole and a tree (two vertical lines because immobile relative to Mr Green). Mr Green's watch indicates 50 in his physically real green 3D space world with Mr Red and his clock ar 43. To illustrate what Mr Red's sequence of 3D worlds is made of I also added a pink bird passing Mr Green when his green wristwatch indicates 43.The content if the events are absolute, observer independent facts, identical for Mr Red and Mr Green. It's amazing some people refute all this by saying: you observe it but it's not what is really (happening) out there, because there is no real Mr Red's 3D world. Mr Red only 'thinks' the green clock is on 43 when his red clock shows 50. Because in LET only the green ether world really exists, Mr Red has no 3D world of his own: Mr Red's simultaneity is only a mathematical feature, nothing physically real. If in LET Mr Red's time and space measurements are no (and can not be) physically real measurements, where is the predictable experimental physical evidence of the LT results? ____________________________________________________ <== How can LET justify physical evidence of green clock with time 43 when red clock shows 50 if the event green clock 43 is not part of the ether world when red clock shows 50 ?
____________________________________________________ <==
I repeat what I said already elsewhere. 1/ Does the time on the red moving clock really run slow? Yes, in Mr Green's physically real 3D space in which Mr Red moves. Not in Mr Red's physically real 3D space. 2/ Does the time on Mr Green's clock really run slow for Mr Red? Yes, in Mr Red's physically real 3D space. Not in Mr Green's physically real 3D space. ____________________________________________________ <==
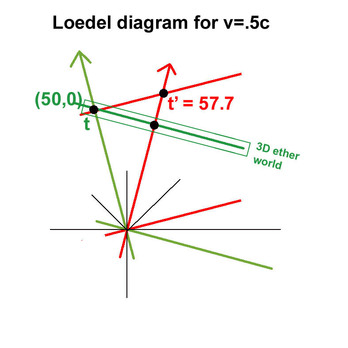
I give you a little discussion with mathematicians and LET adepts pretending LET is experimentally indistinguishable from SR because of the same mathematical result of the LT in LET and SR: LET mathematician: << ... It's more than that; the moving guy also thinks that the clock of the guy at rest relative to the ether is ticking slower than his. "Time dilation" in this sense is still symmetric. It's just that LET gives a privileged status to the guy at rest relative to the ether; his perception is the "true" one, and the perception of the moving guy, who thinks the guy at rest's clock is ticking slower, is an "illusion" >>. Question : << Can you show us how that (bold) works? I reckon in LET the moving guy is rather observing slower ether time? You say 'thinks'. I'm interested what is out there in 3D space. Physics. Not what he thinks... >> Mathematician: << Easy. The laboratory has a set of local rods and local clocks which are synchronized using light signals in the laboratory frame. According to LET these are related by the LT to the true time and space coordinates in the ether frame. I will denote local coordinates as the primed coordinates and the aether coordinates by unprimed variables. A clock at rest at the origin of the ether frame has a constant position x=0. So by the LT in the lab frame it reads time: t' = γ (t-vx/c²) = γt Since γ>1 the aether clock appears to run slow according to the local clocks. >> (Be careful; t'=γt is the time dilation in red's frame, not in green's frame in which t=γt') There is a word that perturbes me: 'appear' !? This is no proof for reciprocity in the Ether: t (50 in sketch) is indeed part of the ether, but t' (57.7 in the sketch), from where the red observer 'measures' to read slower green, is not part of the ether! In the ether context the t'=57.7 is fictitious. The mathematical 'proof' is simply confirming that in the ether context (LET) Mr Red measures from his 'illusion bubble' ! Great physics! It is true that t'= γt Mathematically that's correct. But LET can not give a physical explanation. In LET there is no physically real laboratory 3D world with the slower stationary clock time indication t slower relative to lab clock time indication t'. In LET the reciprocity of time dilation and length contraction is a mental illusion, given by a mathematical result of fictitious primed coordinates. Lorentz: (my bold) << The chief cause of my failure was my clinging to the idea that the variable t only can be considered as the true time and that my local time t' must be regarded as no more than an auxiliary mathematical quantity. In Einstein's theory, on the contrary, t' plays the same part as t; if we want to describe phenomena in terms of x'; y'; z'; t' we must work with these variables exactly as we could do with x; y; z; t. >> Lorentz, H.A (1916), The theory of electrons, Leipzig & Berlin: B.G. Teubner Therefore in LET you may not say that for Mr Red when the physically real red clock time t' indication shows 50, the green one shows 43. You do not have any 'experimental or observational evidence' for that. You only have mathematical 'evidence(?)' using fictitious numbers. Mathematicians will tell you that: << LET and SR (block universe) have the same math and they predict the same outcome for any experiment, so they are physically indistinguishable and equally supported by the evidence. The choice of interpretation is one of personal philosophy, not physics. >> Sigh. Actually it's very easy to write this kind of polished literature, but how does this makes sense? How can they predict the same evidence? How can they be physically indistinguishable? And how equally supported by evidence? They never tell you how that works. Look what another LET fanatic might respond as far as experimental evidence in SR and LET is concerned: << Both SR and LET use the same Lorentz transforms and therefore they both make the exact same predictions for all measurements. Therefore, despite their important differences, they are empirically indistinguishable. You have still failed to even attempt to propose any experimental measurement where SR and LET predict different quantitative results. >> Where can there be 'observational evidence' if the moving frame's (primed) time and space coordiates are not physically real? Making physical measurements or observations of fictitious simultaneity might make sense on your calculator, but not in physics. Experimental real life evidence will indeed always confirm the results of the LT. But not because LET is an option. Only because SR is true. In next chapter I will show you why the LT results can only measure constant speed of light in SR, not LET. You can prove anything with fictitious data or concepts. Einstein uses physically real primed and unprimed coordinates: the 'moving' observer's simultaneous space-like events are physically simultaneously real. Period. Only SR shows the physical equivalence of all inertial systems. Therefore it is a misconception that both LET theory and SR are equally valid theories because they deal with the same mathematics of the Lorentz Transformations. That's refuting the difference between physics and mathematics. Richard Feynman: <<... Physics is not mathematics, and mathematics is not physics. One helps the other. But you have to have some understanding of the connection of the words with the real world..>> (at minute 45:42: click here) Galilean transformations confirm Newtons (and Lorentz's) absolute 3D (ether) space. After transformation you are not forced to drop the ether to make sense of the transformation coordinates. But with Lorentz Transformations that doesn't work. Lorentz Transformations need physically real 4D Spacetime existence (Block Universe). << From a "happening" in three-dimensional space, physics becomes, as it were, an "existence" in the four-dimensional "world". >> Albert Einstein. "Relativity: The Special and the General Theory." 1916. Appendix II Minkowski's Four-Dimensional Space ("World") (supplementary to section 17 - last section of part 1 - Minkowski's Four-Dimensional Space). << Since there exists in this four dimensional structure [space-time] no longer any sections which represent "now" objectively, the concepts of happening and becoming are indeed not completely suspended, but yet complicated. It appears therefore more natural to think of physical reality as a four dimensional existence, instead of, as hitherto, the evolution of a three dimensional existence. >> Albert Einstein. "Relativity." 1952. |
|
-
=> Go to ....
- Introduction
- Relativity for Dummies
- 4D Spacetime Block Universe
- Reciprocal time dilation
- Reciprocal length contraction
- Lengths do not 'appear' contracted!
- Measuring the contracted train
- Constant light speed
- Where is the bullet?
- Train experiment
- Slower and shorter - case study
- Minkowski vs Loedel
- Spacetime video
- Further reading